RAZONES TRIGONOMÉTRICAS DE 30° 60° -45° 45° -37 53° PROBLEMAS RESUELTOS
OBJETIVOS :
❖ Definir las razones trigonométricas para ángulos notables.
❖ Reconocer la proporcionalidad de los lados del triángulo rectángulo de ángulos agudos.
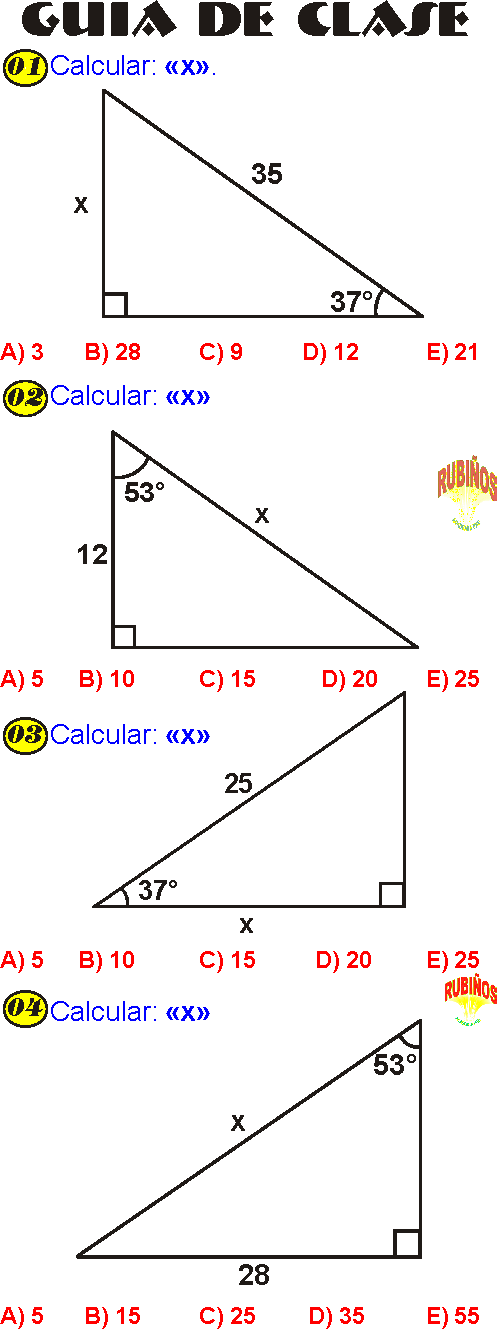
❖ Definir las razones trigonométricas de los ángulos de 30º – 60º; 45º; 37º – 53º.
❖ Detectar gráficamente la proporcionalidad de los triángulos rectángulos notables.
EJERCICIO 1 :
Calcule: sen37°.sec53°
EJERCICIO 2 :
Calcule: cos37°.csc53°
EJERCICIO 3 :
Calcule: ctg37°.ctg53°
EJERCICIO 4 :
Calcule: sec37°.sec53°