TRIGONOMETRIA ESFERICA PROBLEMAS RESUELTOS
TRIÁNGULO POLAR O SUPLEMENTARIO
El triángulo polar de un triángulo esférico es otro triángulo esférico que se obtiene por arcos de circunferencias máximas cuyos polos son los vértices del triángulo dado.
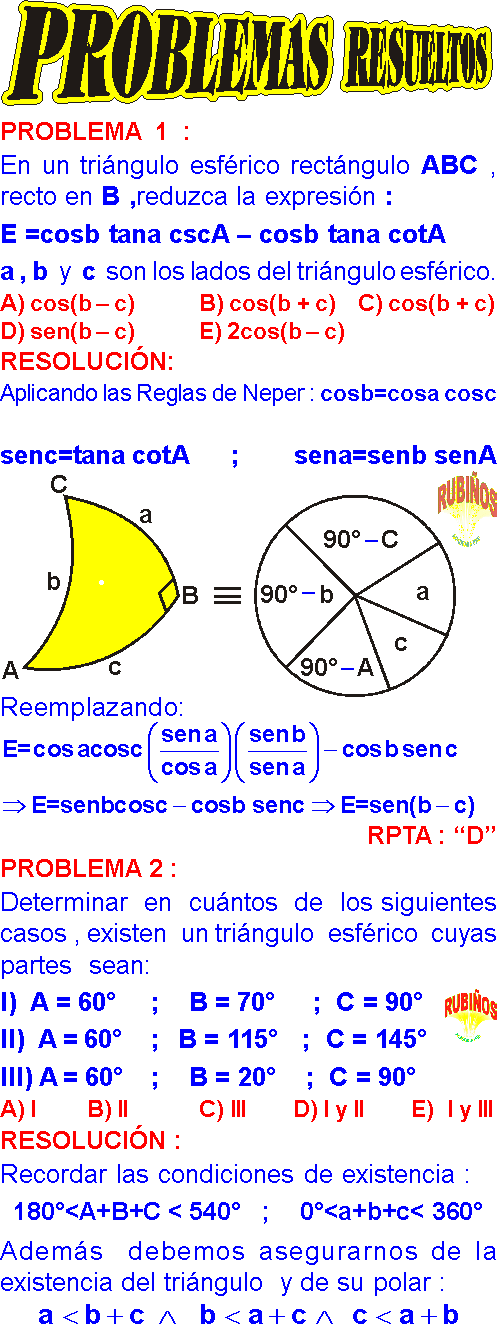
El exceso esférico de un triángulo trirrectángulo es E. Calcular : A) 2 B) 3 C) 3/2 D) 5/2 E) 7/3 REsolución : Sea ABC el triángulo esférico , como es trirrectángulo: A = B = C = 90°, luego el exceso : Se Pide : RPTA : ‘‘d’’ PROBLEMA 4 : En un triángulo esférico ABC de lados a , b y c. Determinar el valor de : donde E y E’ son los excesos esféricos del triángulo ABC y su polar respectivamente . A) 1 B) –1 C) –2 D) 0 E) 2 RESolucion : Sabemos: E = A + B + C – 180° Þ A+ B+ C = 180°+ E Tomando ‘‘cosenos’’ : cos(A+B+C)= cos(180°+ E) Þ cos(A+B+C)=– CosE Para el triángulo Polar : E’= A’+B’+C’–180° E’ = (180° – a) + (180° – b) + (180° – c) –180° Þ a + b + c= 360° – E’ Tomando ‘‘cosenos’’ : En ‘‘M’’ : RPTA : ‘‘b’’ PROBLEMA 5 : Se tiene el triángulo esférico ABC , tal que a =30°, b=42°, c=48°. Determinar ‘‘n’’ en la relación : Donde : SA,B,c, = Área del triángulo polar de ABC S = Área de la esfera que contiene a ABC A) 1 B) 3 C) 4 D) 7 E) 2 RESolucion : Triángulo ABC : a = 30° ; b = 42° ; c = 48° Þ Perímetro : P = 30°+ 42°+ 48°= 120° Sabemos: ....(Exceso del Polar) Reemplazando : E’= 360° – 120°= 240° área del Polar : área de la Esfera Por dato : RPTA : ‘‘b’’